NOTASI SIGMA, BARISAN&DERET, INDUKSI MATEMATIKA

1. Notasi Sigma 
Notasi sigma adalah sebuah tanda yang digunakan untuk menuliskan penjumlahan secara singkat. Notasi sigma, ditulis dengan  
Secara umum, notasi sigma didefinisikan sebagai berikut : 
 
Dimana: 

i adalah indeks penjumlahan

n adalah batas bawah penjumlahan

n adalah batas atas penjumlahan

Sifat-sifat notasi sigma: 
 
 
 
 
 
Contoh : 
Tentukan  
Jawab: 
 
2. Barisan dan Deret Aritmatika 
Suatu barisan  disebut barisan aritmatika jika selisih antara dua suku yang berurutan selalu tetap, selisih tersebut dinamakan beda yang dilambangkan dengan “b”. 
 
Jika suku pertama dinyatakan dengan a, maka bentuk umum barisan aritmatika adalah : 
 
Apabila a menyatakan suku pertama, n menyatakan banyak suku dan bmenyatakan beda, maka : 
1. Suku ke – n barisan aritmatika (U_n) dirumuskan sebagai : 
 

2. Jumlah n suku pertama deret aritmatika (S_n) dirumuskan sebagai: 
 

3. Untuk n ganjil, maka suku tengah barisan aritmatika (U_t) dirumuskan sebagai:  

4. Sisipan dalam deret aritmatika 
 
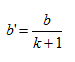
dimana : b = beda sebelum di sisipi, b'= beda yang baru setelah disisipi 

5. Banyaknya suku baru setelah disisipi (n') 
 
6. Jumlah n suku pertama sesudah sisipan 
 

Contoh: 
1. Diketahui barisan aritmatika 5, 8, 11, ...., 125, 128, 131. Suku tengahnya adalah ..... 
Jawab: 

Barisan aritmatika : 5, 8, 11, ……, 131
a = 1 , Un = 131 

suku tengah : 
 

2. Jumlah n buah suku pertama suatu deret aritmatika dinyatakan oleh  Beda deret tersebut adalah: 
Jawab: 
 
 
3. Berapakah jumlah semua bilangan-bilangan bulat diantara 100 dan 300 yang habis dibagi oleh 5? 
Jawab: 
Barisan diantara 100 dan 300 yang habis dibagi 5 ;
105, 110, 115, ....., 295 
a = 105, b = 5 dan Un = 29

Un = a + (n – 1) . b 

295 = 105 + (n – 1) . 5 

190 = 5n – 5 

5n = 195 

n = 39

3. Barisan dan Deret Geometri Suatu barisan geometri jika perbandingan antara dua suku yang berurutan ( r ) selalu tetap. 
 
Rasio yang baru setelah deret geometri disisipi k bilangan adalah : 

Untuk n ganjil, suku tengah barisan geometri :
 
Contoh: 1. Diketahui barisan geometri 1, 2, 4, 8, ...... Bila jumlah n suku pertama, adalah 2047, berapakah U_t ? 
Jawab : 
1, 2, 4, 8, ......
a = 1, r = 2 , Sn = 2047 
Karena r > 1, maka : 
 
 
2. Suku kelima dan suku kedelapan suatu barisan geometri berturut-turut adalah 48 dan 384. Suku keempat barisan tersebut adalah ....
Jawab:

  
Maka: 
 

4. Deret Geometri Tak berhingga 

Pada deret geometri, untuk maka deret tersebut dikatakan deret geometri tak berhingga. Bentuk umum deret geometri tak berhingga adalah sebagai berikut : 
Deret geometri tak berhingga dikatakan konvergen (mempunyai limit jumlah) jika -1 <> 

Jika  maka deret tersebut dikatakan divergen (tidak mempunyai limit jumlah,sehingga : 
Contoh:
suku ke n deret geometri adalah 4^{-n maka jumlah tak berhingga deret tersebut adalah:}